[이산수학]3강. 증명

[출처] 방송통신대학교 이산수학 강의 정리

 

 

학습목표

1. 다양한 증명방법의 종류를 이해하고 때에 따라 적절한 증명방법을 선택할 수 있다.
2. 기본단계와 귀납가정을 설계하고 귀납단계를 통해서 주어진 명제가 타당함을 증명할 수 있다.
3. 직접적으로 명제를 증명하기 어려울 때는 증명하기 쉬운 형태로 주어진 명제를 변경할 수 있다.
4. 전수증명, 조합적 증명법, 컴퓨터를 이용한 증명방법을 이해하고 상황에 따라 증명방법을 사용할 수 있다.

 

 

3.1 기본사항

 

(1)정의

- 공리(axiom) : 어떤 다른 명제들을 증명하기 위해 전제로 사용되는 가장 기본적인 가정으로, 별도의 증명 없이 참(T)으로 이용되는 명제

예1: 두점이 주어졌을 때, 두 점을 통과하는 직선을 그릴 수 있다.(유클리드 기하학)

예2: 어떤 자연수도, 그 수의 다름 수가 존재한다. (페아노의 공리)

예3: 어떤 것도 포함하지 않는 집합이 존재한다. (공리적 집합론)

 

- 증명(proof) : 특정한 공리들을 가정하고, 그 가정하에 제안된 명제가 참(T)임을 입증하는 작업

- 정리(theorem) : 공리로부터 증명된 명제를 정리라고 한다.

1) 보조정리 (lemma) : 정리를 증명하는 과정 중에 사용되는 증명된 명제

2) 따름정리 (corollary) : 정리로부터 쉽게 도출되는 부가적인 명제

 

(2) 증명방법

1) 직접 증명법 : 공리와 정의, 그리고 정리를 논리적으로 직접 연결하여 증명

2) 수학적 귀납법 : 기본단계, 귀납가정, 귀납단계를 이용해 자연수 n에 대한 명제의 성질을 증명

3) 간접 증명법 : 증명해야 할 명제를 증명하기 쉬운 형태로 변형하여 증명

- 대우, 모순, 반례, 존재 증명법 등

4) 그 외 : 전수, 조합적, 컴퓨터 이용 증명법 등

 

 

3.2 직접 증명법

 

- 직접 증명법 ( direct proof)

- 다른 말로 연역법(deduction)이라고 함.

- 연역법 : 이미 증명된 하나 또는 둘 이상의 명제를 전제로 하여 새로운 명제를 결론으로 이끌어내는 것.

 

- 명제를 변형하지 않고 증명하기 때문에 직접 증명법

- 주로, 공리와 정의, 그리고 이미 증명된 정리를 논리적으로 직접 연결해 증명하는 형식을 따른다.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

- 파스칼 삼각형(Pascal`s triangle)

- n, k는 양의 정수이고, k <= n 이라고 가정하면 C(n + 1,k) = C(n,k) + C(n,k +1)

 

파스칼의 삼각형은 수학에서 이항계수를 삼각형 모양의 기하학적 형태로 배열한 것이다. 이것은 블레즈 파스칼에 의해 이름 붙여졌으나 이미 수세기 전에 다른 사람들에게서 연구된 것이다.

단순한 형태로, 파스칼의 삼각형은 다음과 같은 방법으로 만들 수 있다.

1. 먼저 첫 번째 줄에는 숫자 1을 쓴다.
2. 그 다음 줄을 만들려면, 바로 위의 왼쪽 숫자와 오른쪽 숫자를 더한다. 예를 들어, 네 번째 줄의 숫자 1과 3을 더하여 다섯 번째 줄의 4가 만들어진다.

수학적으로, 이 구조는 파스칼의 법칙을 사용하여 아래와 같이 표현한다. n 번째 줄의 k 번째 값을 라고 하면, 이 값은

()

으로 정의된다. 이때,

 

- 일반화 : 파스칼의 삼각형은 더 높은 차원으로 확장하여 일반화할 수 있다. 3차원 형태는 파스칼의 피라미드 또는 파스칼의 4면체로 부른다. 더 높은 차원의 유사체를 일반적으로 총칭하여 "파스칼의 단체"라고 말한다..[출처]위키백과

 

 

 

 

 

 

 

 

 

 

 

 

팩토리얼(factorial) : 수학에서, 계승(階乘, 영어: factorial 팩토리얼^[*], 문화어: 차례곱)은 1부터 까지의 연속된 자연수를 차례로 곱한 값이다. 기호로는 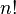과 같이 느낌표(!)를 사용하며, 이는 한국에서 간혹 "팩"으로 읽는 경우가 있다. 이를테면 3!은 "3팩"이 된다. .[출처]위키백과

 

 

 

 

 

 

 

 

 

3.3 수학적 귀납법

- 모든 자연수 n에 대해 명제를 증명하는 데 유용

- 3단계 과정

- 기본단계 : n의 출발점에서 명제가 성립하는가 확인

- 귀납가정 : n=k일 때 명제가 성립한다고 가정

- 귀납단계 : n=k+1일 때도 명제가 성립함을 증명

 

 

 

- 수학적 귀납법(數學的歸納法, 영어: mathematical induction), 줄여서 귀납법은 어떤 성질이 모든 자연수에 대해 성립함을 증명하기 위해 사용되는 방법이다. 첫 자연수에 대해 참인 것과, 어떤 자연수에 대해 참이면 항상 다음 자연수에 대해서도 참인 것을 증명하는 두 과정으로 이루어진다.

보다 일반적으로, 이는 모든 순서수의 모임에 대한 초한귀납법으로 확장할 수 있으며, 임의의 기초관계에 대한 구조적 귀납법으로 확장할 수도 있다.

수학적 귀납법에 의한 증명은, 이름과는 달리 귀납적 논증이 아닌 연역적 논증에 속한다. 이러한 증명의 합리성을 기술하는 수학적 귀납법의 원리는, 페아노 공리계의 공리 중 하나이며, 메타논리적 추론 규칙이기도 하다 .[출처]위키백과

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3.4 간접 증명법

1) 대우 증명법 (proof by transposition)

 

 

 

 

 

 

         2) 모순증명법 (proof by contradiction)

 

 

 

 

 

 

3) 반례증명법

 

 

 

 

 

 

 

 

4) 구성적 존재증명법

- 명제함수 ∃xP(x)를 증명할 때 P(x)를 참으로 만드는 x를 찾거나 찾는 과정을 제사함.

 

 

 

 

 

 

 

5) 비구성적 존재증명법

- 명제함수 ∃xP(x)를 증명할 때 P(x)를 참으로 만드는 x를 찾지 않고 우회적으로 명제가 타당함을 보이는 방법

 

 

 

 

 

 

 

 

 

 

 

 

3.5 다양한 증명방법

1) 전수 증명법

- 명제에서 유도될수 있는 경우의 수가 적을 때 일일이 모든 경우의 수를 조사하는 방법

 

 

2) 조합적 증명법

- 두 집합의 원소의 개수가 동일함을 증명할 때 사용됨

 

1) 전단증명

- 원소가 n개인 집합 A와 원소그 m개인 집합 B를 찾은 후, 두 집합이 일대일 관계임을 보여 n=m임을 증명함.

 

2) 증복산정

- 동일한 집합의 원소를 두 가지 방법으로 센 다음, 그 결과가 각각 n과 m이라면 n=m임을 증명함.

 

 

3) 컴퓨터를 이용한 증명

- 증명하기가 복잡한 경우

- 컴퓨터의 데이터 처리 능력을 이용하여 증명함.

 

- 4색 정리

- 평면을 유한개의 부분으로 나누어 각 부분에 색을 칠할 때, 서로 맞닿은 부분을 다른 색으로 칠한다면 네가지 색으로 충분하다.